Problem Statement – To economically design a carton box to pack 20 half litre pouches
Regular Slotted Carton
Carton box is formed from regular slotted carton (RSC). The image shows how a cardboard is cut to form a carton box.
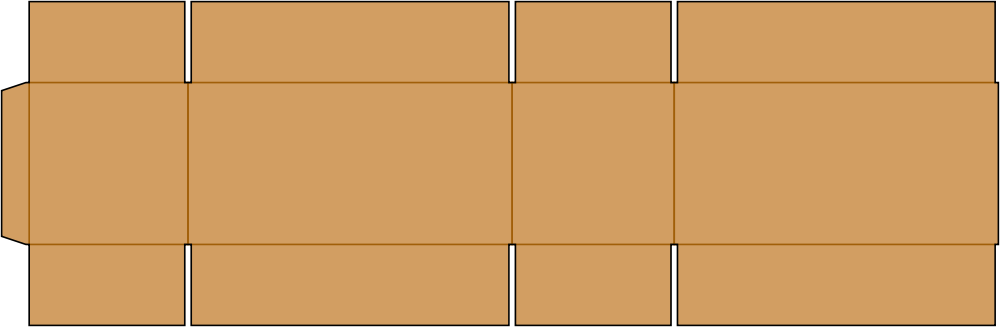Solution
If l is the length, b the breadth and h the height of a formed carton box, then the area of the cardboard shown above is 2 * (l + b) * (b + h). Cost of the carton box is directly proportional to the area of the card board used. So, the problem boils down to reducing the area of cardboard for a given volume of carton box.
Minimise 2 * (l + b) * (b + h), given l * b * h = V, a constant
Ideally, the surface area of any cuboid is 2*(l*b + b*h + l*h), but there is an extra 2b2 area in the figure. That extra area becomes the inside flaps during forming of carton box. It gives additional strength to carry load inside the carton box. Also, in order to avoid that area, the card board has to be cut into a more complex shape. With that area, cutting the card board is a simple i.e. a rectangle of length 2*(l + b) and breadth (b + h).
We know that, the cuboid with minimum surface area for a given volume is a ‘cube’. But that is not the case here as there is extra 2b2 area.
Let F(l, b, h) = (l + b) * (b + h) = lb + lh + b2 + bh Ignore the factor 2 for time being
To eliminate factor ‘l’ from the expression, substitute l = V/bh (Since lbh = V)
F(b,h) = V/h + V/b + b2 + bh
Differentiate partially w.r.t. ‘h’, Fh(b,h) = -V/h2 + b
Equating to zero, we get, b = V/ h2
Substituting for V = lbh, we get, b = lbh/h2 or l = h.
Rewriting the problem, by substituting l = h, we get,
V = bh2
Area = 2 * (h + b)2
(h + b)2 is minimum when (h + b) is minimum, since (h+b) can’t get negative.
Minimise (h + b), given bh2 = V
Let, F(b,h) = h + b
We can eliminate the variable b by substituting for b = V/h2
F(h) = h + V/ h2
On differentiation, F’(h) = 1 – 2V/h3
Equating to zero, we get, h3 = 2V or h = (2V)1/3
Now, b = V/h2 or b = (V/4)1/3
For optimal solution, l = (2V)1/3, b = (V/4)1/3 and h = (2V)1/3
In our case of 500 ml pouches, though the volume of coconut oil is 10 litres, about 25% allowance should be given to accommodate the pouch film, and the pouch though flexible is not a perfect fluid to occupy all the space inside the box. So, the volume of carton box required is 12.5 litres or 12500 cubic cms. So, the dimensions of carton box area l = 29.24 cms, b = 14.62 cms and h = 29.24 cms for V = 12500.
Comparison
At present, we are using the standard sized carton box for both half litre and one litre pouches. We don’t have any other option now as our order quantities are small.
l = 32, b = 19 and h = 21, V = 12768 cm3 and A = 4080 cm2
For V = 12768, with minima solution, we have just arrived, l = 29.45, b = 14.72, h = 29.45 A = 3902 cm2
Or the ideal solution is 4.35% better. It may look insignificant but carton box is a packing raw material with repeated use and large quantity. So, it can result in significant cost savings. At Cocoguru, we examine each of these items for its costs and try and minimise it without compromising on customer value.
Cutting Costs is not about Cutting Corners but about careful Value Engineering.
