Cocoguru brand has been built to benefit the farmers and consumers. It is successfully delivering quality coconut oil to consumers, who have been repaying their faith in us. The brand is growing stronger by the day, it is getting into newer territories, adding more products, and improving its quality. You don’t have to blindly believe us or the rumours, you may consider the following points before you form an opinion:
Premium product
Cocoguru brand is sold at a premium compared to other brands in the local market. So, cutting costs by adulteration is not necessary. It is not sustainable to sell at a premium by delivering inferior adulterated products.
Read more: cocoguru.com/yet-another-price-increase/
Brand
We believe in the power of the brand. We appreciate the fact that the brand as an asset is more valuable than all the physical assets like land, buildings, plant & machinery, saleable inventory, etc. So, every activity we do should be towards building and nurturing the brand. Adulteration or shortcuts are the quickest ways to kill it. Cocoguru brand is already 14 years old and is built to last. We are in it for the long term, not just for short-term profits.
Read more: cocoguru.com/adulteration-in-coconut-oil/
Consumer push instead of retailer push
Cocoguru products are sold because of demand by consumers at retail stores. In contrast to push by retailers for their benefit. To sustain this cycle, we should continue to satisfy and delight consumers rather than bribe retailers with better margins and payment terms.
Read more: cocoguru.com/how-do-we-set-mrp/
Sold at Super Markets and eCommerce portals
High-end quality-conscious consumers buy our products through modern trade supermarkets and various e-commerce portals. Our challenge is to stand their scrutiny of quality and standards. They don’t stress us on prices and hence there is no need for adulteration.
Read more: cocoguru.com/cocoguru-is-now-available-at-reliance-smart-stores/
User reviews
Don’t believe what we say, better to believe what other users have to say. In the days of social media and user-generated content, people are happy to review and recommend products based on their experience. Check the reviews and comments on social media platforms like Facebook & Instagram, and eCommerce portals like Amazon & Flipkart. At the Amazon portal, 1000s of consumers buy coconut oil from us every month, and almost 3000 consumers have reviewed the products with a 4.3 to 4.4-star average rating. Check our standings in the best sellers rank for coconut oil, it is in the top 20 list and among the top 8 brands in the country.
fssai random checks
Food Safety department conducts random tests of food products from the market. They don’t inform us, they test for the quality at the CFTRI laboratory and take actions based on their report. This way fssai is supposed to ensure that the food product consumers buy from the market is safe. Our products have been picked and tested at Kasaragod, Udupi, Mangaluru, Chikkamagaluru, and Kodagu and are safe every time. Yes, the department officials take bribes from brands and restrain them from taking action against brands if they get satisfactory amounts from them. However, Kerala’s food department is very strict with coconut oil as it is their staple edible oil. They have listed a widely sold coconut oil from Karnataka as adulterated.
Read more: indiafilings.com/learn/fssai-food-testing-procedure/
Laboratory testing
If you are not convinced, take a random sample yourself and test it against the parameters listed by BIS for coconut oil at any laboratory and find the results for yourselves. The test parameters and the results we obtained are here.
Full accounting and Invoicing
All the transactions carried out at Cocoguru are accounted for and audited by multiple government revenue departments like Income Tax, GST, APMC, Labour, Factories, Food, etc. All the transactions carry a legal Invoice or document. So, they can be traced and scrutinized.
Read more: cocoguru.com/statutory-info/
Transparency and Information
We believe in transparency and all the information is easily available to anyone who seeks it. We don’t fear competitors copying the ideas as that alone won’t give them the success that we have achieved. Our website is highly informative and detailed, our social media pages are continuously updated and informative. Only when we are confident of our activities, and it is good for the consumers do we share our information.
Factory Visit
We work from 9:00 am to 6:00 pm from Monday to Saturday. Anyone interested is welcome to visit the oil mill. No need to inform us, just randomly visit. Randomness of visits gives us no scope for any special “preparation”, Experience the cleanliness, methodical process, quality of raw materials and finished products. Ask us if you have any queries about the products and processes, and we will be happy to answer them whether you buy the product or not.
Read more: cocoguru.com/infrastructure/
Dimensions of the most economical Carton Box
Problem Statement – To economically design a carton box to pack 20 half litre pouches


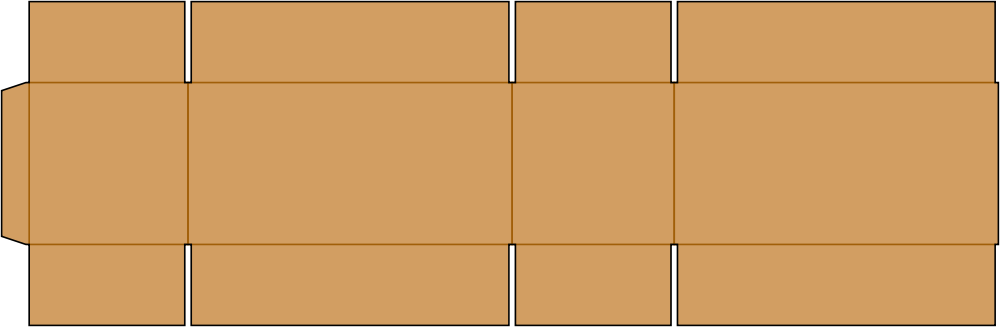
Regular Slotted Carton
Carton box is formed from regular slotted carton (RSC). The image shows how a cardboard is cut to form a carton box.
 Solution
Solution
If l is the length, b the breadth and h the height of a formed carton box, then the area of the cardboard shown above is 2 * (l + b) * (b + h). Cost of the carton box is directly proportional to the area of the card board used. So, the problem boils down to reducing the area of cardboard for a given volume of carton box.
Minimise 2 * (l + b) * (b + h), given l * b * h = V, a constant
Ideally, the surface area of any cuboid is 2*(l*b + b*h + l*h), but there is an extra 2b2 area in the figure. That extra area becomes the inside flaps during forming of carton box. It gives additional strength to carry load inside the carton box. Also, in order to avoid that area, the card board has to be cut into a more complex shape. With that area, cutting the card board is a simple i.e. a rectangle of length 2*(l + b) and breadth (b + h).
We know that, the cuboid with minimum surface area for a given volume is a ‘cube’. But that is not the case here as there is extra 2b2 area.
Let F(l, b, h) = (l + b) * (b + h) = lb + lh + b2 + bh Ignore the factor 2 for time being
To eliminate factor ‘l’ from the expression, substitute l = V/bh (Since lbh = V)
F(b,h) = V/h + V/b + b2 + bh
Differentiate partially w.r.t. ‘h’, Fh(b,h) = -V/h2 + b
Equating to zero, we get, b = V/ h2
Substituting for V = lbh, we get, b = lbh/h2 or l = h.
Rewriting the problem, by substituting l = h, we get,
V = bh2
Area = 2 * (h + b)2
(h + b)2 is minimum when (h + b) is minimum, since (h+b) can’t get negative.
Minimise (h + b), given bh2 = V
Let, F(b,h) = h + b
We can eliminate the variable b by substituting for b = V/h2
F(h) = h + V/ h2
On differentiation, F’(h) = 1 – 2V/h3
Equating to zero, we get, h3 = 2V or h = (2V)1/3
Now, b = V/h2 or b = (V/4)1/3
For optimal solution, l = (2V)1/3, b = (V/4)1/3 and h = (2V)1/3
In our case of 500 ml pouches, though the volume of coconut oil is 10 litres, about 25% allowance should be given to accommodate the pouch film, and the pouch though flexible is not a perfect fluid to occupy all the space inside the box. So, the volume of carton box required is 12.5 litres or 12500 cubic cms. So, the dimensions of carton box area l = 29.24 cms, b = 14.62 cms and h = 29.24 cms for V = 12500.
Comparison
At present, we are using the standard sized carton box for both half litre and one litre pouches. We don’t have any other option now as our order quantities are small.
l = 32, b = 19 and h = 21, V = 12768 cm3 and A = 4080 cm2
For V = 12768, with minima solution, we have just arrived, l = 29.45, b = 14.72, h = 29.45 A = 3902 cm2
Or the ideal solution is 4.35% better. It may look insignificant but carton box is a packing raw material with repeated use and large quantity. So, it can result in significant cost savings. At Cocoguru, we examine each of these items for its costs and try and minimise it without compromising on customer value.
Cutting Costs is not about Cutting Corners but about careful Value Engineering.
